Pravítko
iNula 15
Řešením šifry je poloha v okruhu 2 km od 49.2020669N, 16.5340519E.
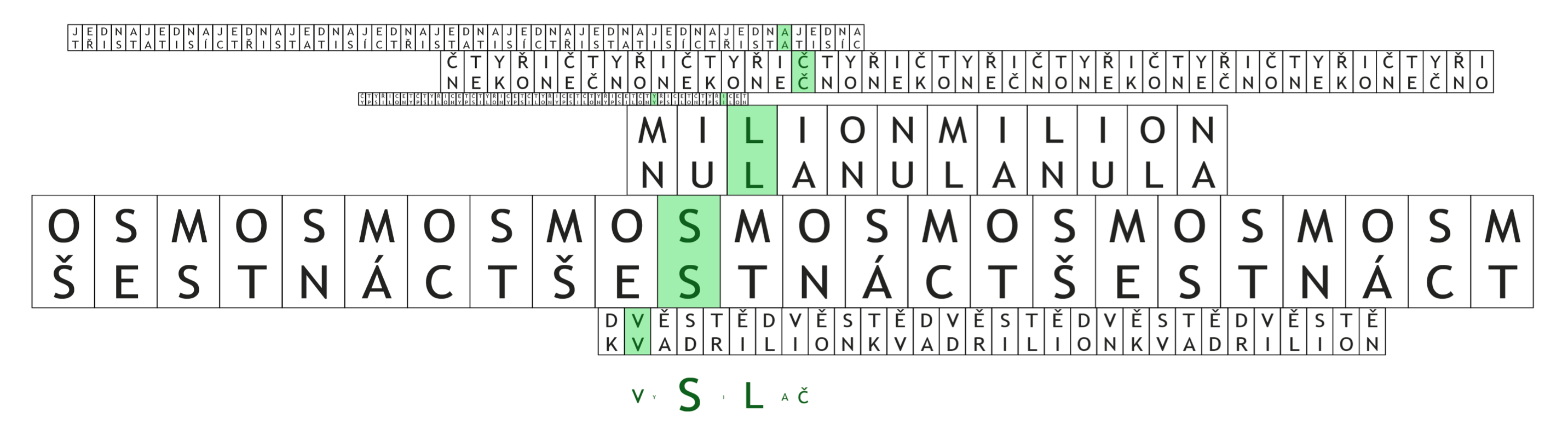
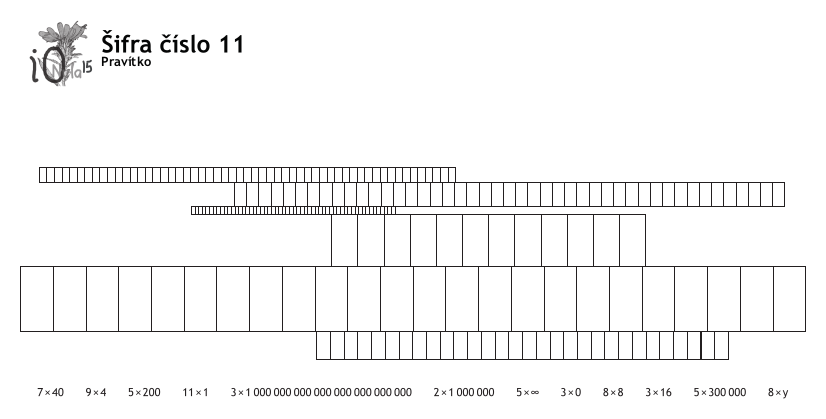
Šifra má dvě části, sadu navazujících mřížek či pravítek s velice rozdílnou velikostí dílků a výrazy tvaru něco × něco. Všimneme si několika věcí.
První činitel ve výrazu je vždy rozumné malé číslo. Druhý činitel být prapodivný: nekonečno, kvadrilion nebo y. Nemá smysl násobit numerickou hodnotu (u 0 ani ∞ se nezmění), budem násobit nějakou jinou vlastnost čísla. Výrazů je navíc přesně dvakrát tolik co pravítek.
To je zajímavé, protože políčka pravítek mají rozměry 2 : 1. Přiřadíme tedy vždy dvě čísla políčkům? Chceme-li políčka něčím vyplnit, nabízí se čísla prostě pojmenovat. Můžeme k tomu dojít i analyticky, když si spočítáme délky pravítek a všimneme si, že jsou dělitelná prvními čísly. Nestačí to sice vždy k jednoznačnému přiřazení, ale např. pro 11 × 1 zřejmě patří do pravítka o 55 polích, protože to je jediný počet dělitelný 11.
Vytvoříme tedy dvojice
| 11 × |JEDNA| | = | 5 × |TŘI STA TISÍC| | = | 55 |
| 9 × |ČTYŘI| | = | 5 × |NEKONEČNO| | = | 45 |
| 7 × |ČTYŘICET| | = | 8 × |YPSILON| | = | 56 |
| 3 × |NULA| | = | 2 × |MILION| | = | 12 |
| 8 × |OSM| | = | 3 × |ŠESTNÁCT| | = | 24 |
| 5 × |DVĚ STĚ| | = | 3 × |KVADRILION| | = | 30 |
a vepíšeme je do políček. Všimneme si, že se v každém pravítku někde objevila společná písmena. Dokonce se každé společné písmeno pojmenování čísel objevilo právě jednou (jak zaručuje čínská věta o zbytcích). Když se podíváme, kde se přesně objevila, zjistíme, že tvoří souvislý blok zhruba uprostřed papíru a příslušná políčka na sebe vodorovně navazují. Promítnutím na základnu – nebo prostě přečtením zleva doprava – dostáváme tajenku VYSILAC.